5-Min Tutorial: K-Means Clustering In Python

K-Means Clustering is a common machine learning tool that allows to separate data into "clusters" (groups). Intuitively, you can imagine plotting each datapoint into a field (could be 2-D,3-D, or n-D field) and then looking at which points are close to which, trying to distinguish groups.

In one of my previous projects in which we analyzed Spam in Soundcloud we actually used K-Means to group together similar types of users. This allowed us to more clearly separate and see groups of musicians, fans, and spam.

Understanding the algorithm

The K-Means algorithm is actually surprisingly intuitive and simple, yet very powerful.

Take a look at the animation below (sorce: David Runyan), as you read through the algorithmic steps.

1. Select number of clusters (refereed to as K) and randomly assign the center points of this clusters anywhere near your dataset points.
2. Update Cluster Assignments: For each point in the dataset, find which is the closest cluster and assign that point to it.
3. Update Cluster Center: For each point in a given cluster, find the average center between them all and choose that to be the new cluster center.
4. Repeat step 2 and 3 until the cluster centers are no longer changing. Convergence tends to be surprisingly quick for most datasets.

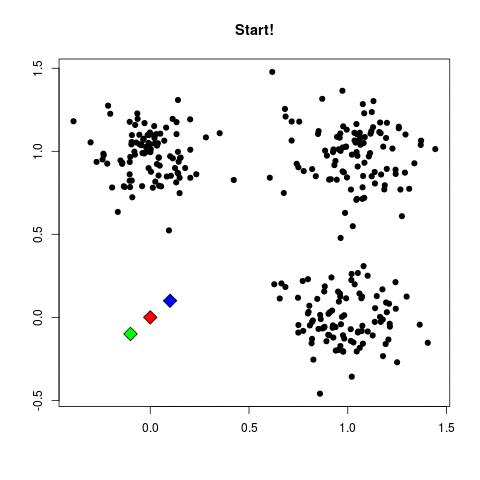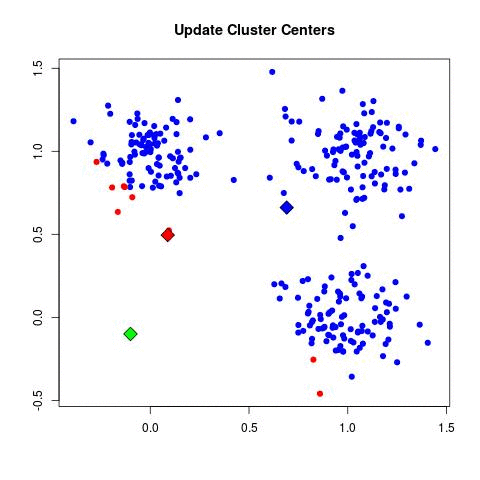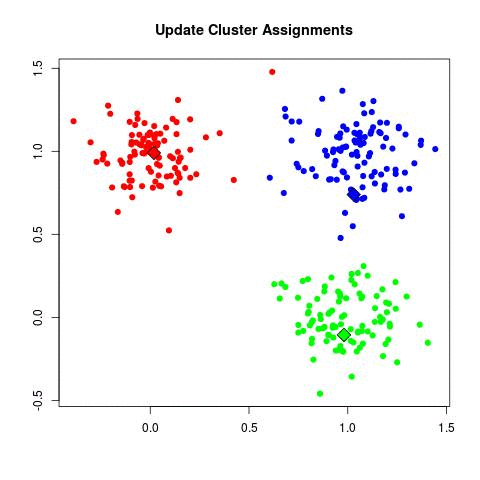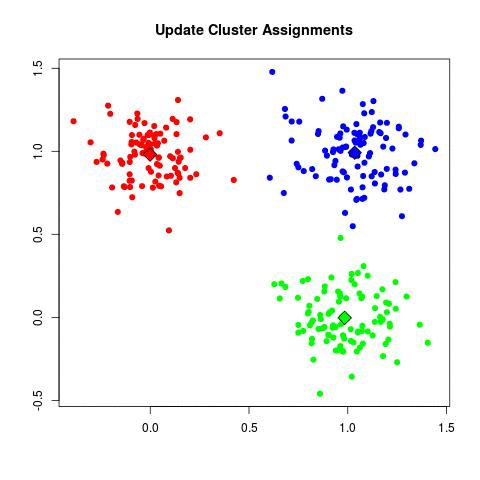
Coding the algorithm

The first thing we will do is define a distance function. In our case a simple Euclidean Distance function will be more than enough. Notice that we want to allow for any number of dimensions.

#Euclidian Distance between two d-dimensional points
def eucldist(p0,p1):
    dist = 0.0
    for i in range(0,len(p0)):
        dist += (p0[i] - p1[i])**2
    return math.sqrt(dist)

Next, we want to code the actual K-Means algorithm. Initially we will designate an max # of iterations and randomly choose centers for the clusters. I like choosing a random datapoint as my center, as it makes things simpler.

#K-Means Algorithm
def kmeans(k,datapoints):

    # d - Dimensionality of Datapoints
    d = len(datapoints[0]) 
    
    #Limit our iterations
    Max_Iterations = 1000
    i = 0
    
    cluster = [0] * len(datapoints)
    prev_cluster = [-1] * len(datapoints)
    
    #Randomly Choose Centers for the Clusters
    cluster_centers = []
    for i in range(0,k):
        new_cluster = []
        #for i in range(0,d):
        #    new_cluster += [random.randint(0,10)]
        cluster_centers += [random.choice(datapoints)]

        #Sometimes The Random points are chosen poorly and so there ends up being empty clusters
        #In this particular implementation we want to force K exact clusters.
        #To take this feature off, simply take away "force_recalculation" from the while conditional.
        force_recalculation = False

We will now start the clustering loop, which will only end if we reach Max_iterations or when our clusters stop changing.

    while (cluster != prev_cluster) or (i > Max_Iterations) or (force_recalculation) :
        
        prev_cluster = list(cluster)
        force_recalculation = False
        i += 1

Next, for every point in the field we will find which is the closest cluster center to it and have it align itself with it.

        #Update Point's Cluster Alligiance
        for p in range(0,len(datapoints)):
            min_dist = float("inf")
            
            #Check min_distance against all centers
            for c in range(0,len(cluster_centers)):
                
                dist = eucldist(datapoints[p],cluster_centers[c])
                
                if (dist < min_dist):
                    min_dist = dist  
                    cluster[p] = c   # Reassign Point to new Cluster

Then we will update the cluster's center position. This is done by taking the average position of all the points in the given cluster. Notice that if we find a cluster which has 0 members, we force the center to randomly move to a new spot. (This is done because we want to enforce the number of centers to be k, and once a cluster has no members, there is no way to add new members to it.)

        #Update Cluster's Position
        for k in range(0,len(cluster_centers)):
            new_center = [0] * d
            members = 0
            for p in range(0,len(datapoints)):
                if (cluster[p] == k): #If this point belongs to the cluster
                    for j in range(0,d):
                        new_center[j] += datapoints[p][j]
                    members += 1
            
            for j in range(0,d):
                if members != 0:
                    new_center[j] = new_center[j] / float(members) 
                
                #This means that our initial random assignment was poorly chosen
                #Change it to a new datapoint to actually force k clusters
                else: 
                    new_center = random.choice(datapoints)
                    force_recalculation = True
                    print "Forced Recalculation..."
                    
            
            cluster_centers[k] = new_center

Finally we can now use our program by simply feeding it a list of datapoints. Notice that these datapoints can be tuples of whatever size one would want. Also you can enforce the number of k clusters too.

#TESTING THE PROGRAM#
if __name__ == "__main__":
    #2D - Datapoints List of n d-dimensional vectors. (For this example I already set up 2D Tuples)
    #Feel free to change to whatever size tuples you want...
    datapoints = [(3,2),(2,2),(1,2),(0,1),(1,0),(1,1),(5,6),(7,7),(9,10),(11,13),(12,12),(12,13),(13,13)]

    k = 2 # K - Number of Clusters
      
    kmeans(k,datapoints) 

Complete Code

This was a fun little script that was surprisingly useful for a couple of homeworks and project that I did last quarter and I thought I would share with you guys. Hopefully you have found this small write-up useful, and as always feel free to contact me with any questions. Cheers!